Pacchetto d'onde

Questa funzione presenta due singolarità:

$\begin{displaymath}f(t)=\left\{ \begin{array}{cc}Fcos(\omega_0 t) & -\tau\leq t \le +\tau\\0 & altrimenti\end{array}\right.\end{displaymath}$

(4)

ed il suo grafico è il seguente:

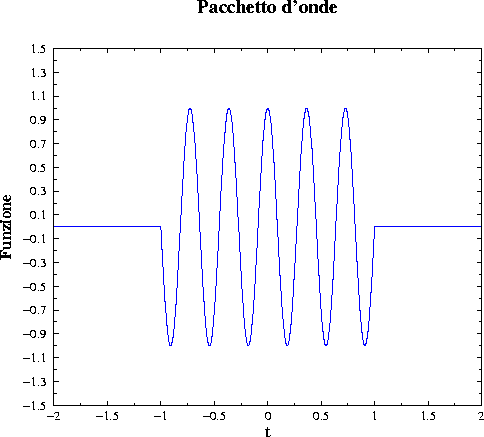
$\begin{figure}\centerline{\epsfig{figure=fcost.eps,width=10cm,angle=-90}}\end{figure}$

La trasformata di Fourier è la seguente funzione:

$\begin{displaymath}F(\omega)=\int_{-\infty}^{+\infty} f(t)e^{i\omega t} dt =2\i......a)} +\frac{sin[(\omega_0+\omega)\tau]}{(\omega_0+\omega)}].\end{displaymath}$

(5)

Il suo grafico è il seguente:

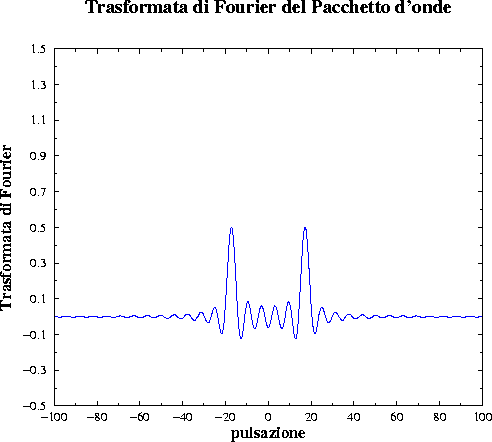
$\begin{figure}\centerline{\epsfig{figure=tcost.eps,width=10cm,angle=-90}}\end{figure}$

Se vuoi leggere dei commenti sui grafici appena visti clicca qui.

L'antitrasformata è il seguente integrale:

$\begin{displaymath}f(t)=\int_{-\infty}^{+\infty} F(\omega)e^{-i\omega t} d\omega \approx2\int_{0}^{\Omega}F(\omega) cos(\omega t) d\omega,\end{displaymath}$

(6)

che va eseguito numericamente fissando il valore della pulsazione di taglio $\Omega$ . Potete visualizzare come la funzione possa essere sempre meglio approssimata all'aumentare di $\Omega$ cliccando ove opportuno.